BWT比对算法
目前二代测序常用的比对软件BWA和Bowtie核心算法都是BWT(Burrows-Wheeler Transform)算法。事实上,BWT是一种数据转换算法,它将一个字符串中的相似字符放在相邻的位置,以便于后续的压缩。
BWT算法可以分为编码和解码两部分。编码后,原始字符串中的相似字符会处在比较相邻的位置;解码就是将编码后的字符串重新恢复成原始字符串的过程。BWT的一个特点就是经过编码后的字符串可以完全恢复成原始字符串。
<1> BWT算法编码部分
本文以GACCTA序列作为参考,进行算法推导。推导的过程如图1所示。
(1) 加标记
在GACCTA序列的右侧加上一个比序列中所有字符的ASCII码都小的标记符号,例如$。
(2) 推导循环矩阵
将标记后字符串的最后一个字符提到最前,组成新的字符串。接着在该字符串基础上,又将最后一个字符提到最前,再次组成一个新的字符串。依次循环,直到标记符号再次回到最后一位。
这些字符串则形成一个所谓的循环矩阵(如图1的循环矩阵列)。
(3) 对循环矩阵排序
根据ASCII码从小到大的顺序,对循环矩阵进行排序(如图1的矩阵排序列)。
(4) 得到循环矩阵的F列和L列
提取排序后的矩阵的第一列字符,作为F列。
提取排序后的矩阵的最后一列字符,作为L列。
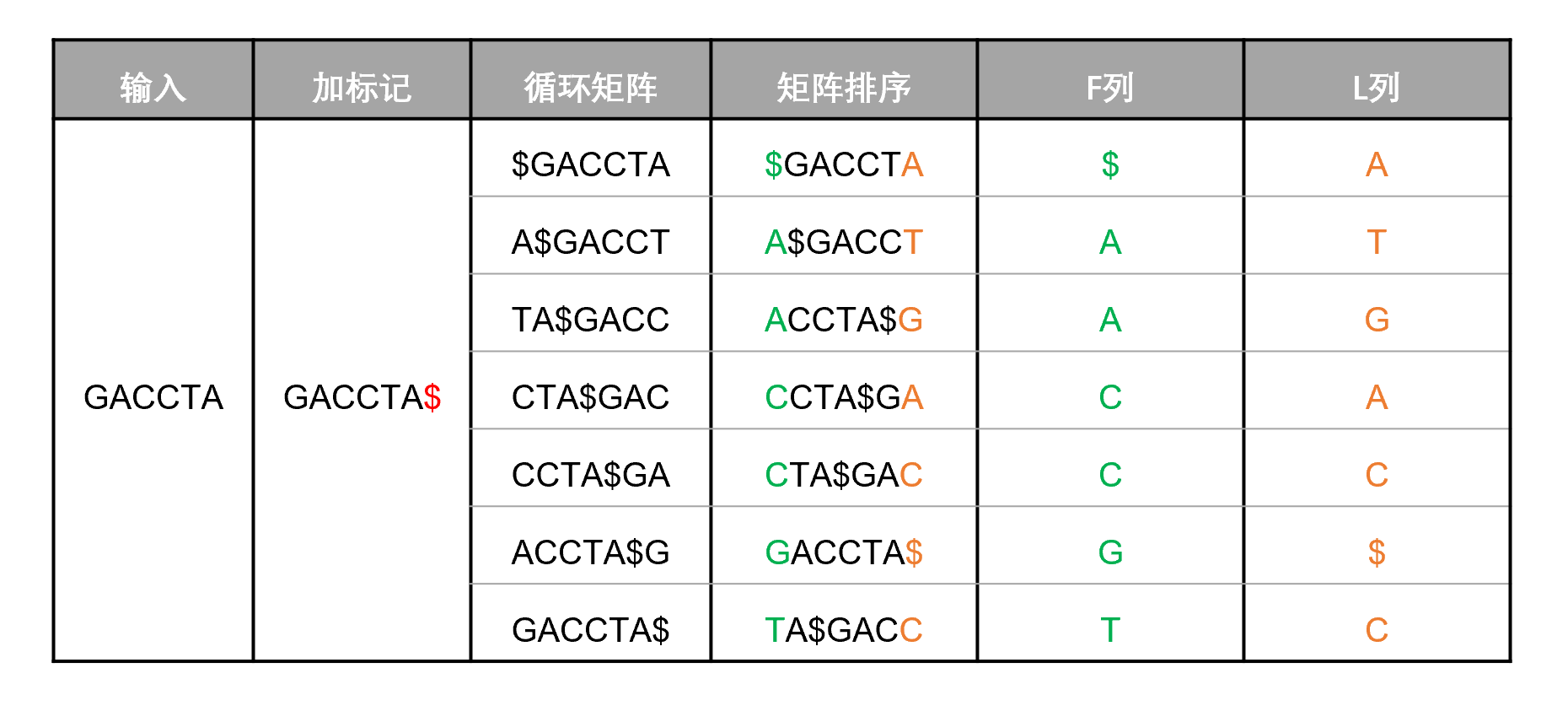
图1 BWT算法编码部分推导过程
<2> BWT算法解码部分
我们以上一步骤得到的F列和L列,回推出GACCTA序列,回推过程如图2所示。
需要注意的是,回推过程是从序列最后一位向第一位进行的,也就是第一个回推出来的字符是A,第二个是T,第三个是C,…,最后一个是G。
(1) 解码起点(回推倒数第一个字符)
(A) 如图2(子图1)所示,我们以L列的标记符号$作为解码的起点。
(B) 在F列找到同样的字符$。
(C) 与F列字符$同一行的L列字符就是解码序列的最后一个字符。这里得到的字符是A。
(2) 回推倒数第二个字符
(A) 以上一步骤L列的A字符作为开始。
(B) 同样的,在F列的寻找相同字符A。然而,可以看到F列并不止存在一个A字符,解决的方案是:A字符在L列是排第几个,就对应F列的第几个。比如这里,A是L列两个A字符的第一个,则对应的也是F列的第一个A字符。
(C) 与F列字符A同一行的L列字符就是解码序列的倒数第二个字符。这里得到的字符是T。
(3) 回推倒数第三个字符
(A) 以上一步骤L列的T字符作为开始。
(B) 同样的,在F列的寻找相同字符T。
(C) 与F列字符T同一行的L列字符就是解码序列的倒数第三个字符。这里得到的字符是C。
(4) 回推的终点
如上述步骤,依次回推,直到最后在L列得到的字符是$标记符时,回推结束。
从图2可以看到,最后得到的序列GACCTA是正确的。
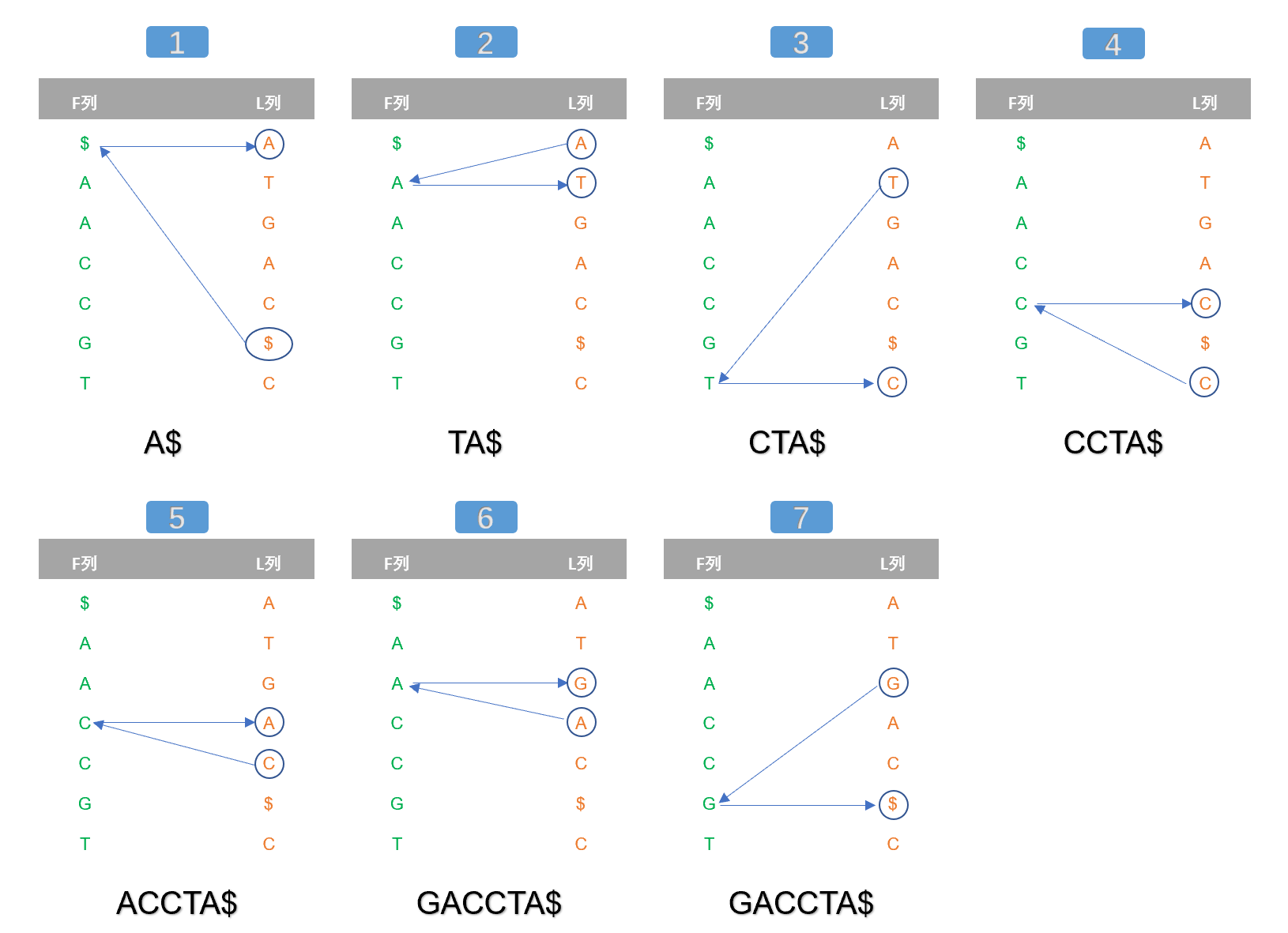
图2 BWT算法解码部分推导过程
<3> 序列比对案例
假设上面所用的序列GACCTA是参考序列,我们模拟将CAA比对到这个参考序列上的过程。
与解码过程一样,比对也是从后向前进行,因此第一个比对的字符是A。
然而,可以在L列上发现有两个A字符,分别以两个字符进行比对。如图3所示,分别比对到CAG和CCA两个位置。然后根据自行定义的打分系统,排除错误的CAG,保留正确的CCA。
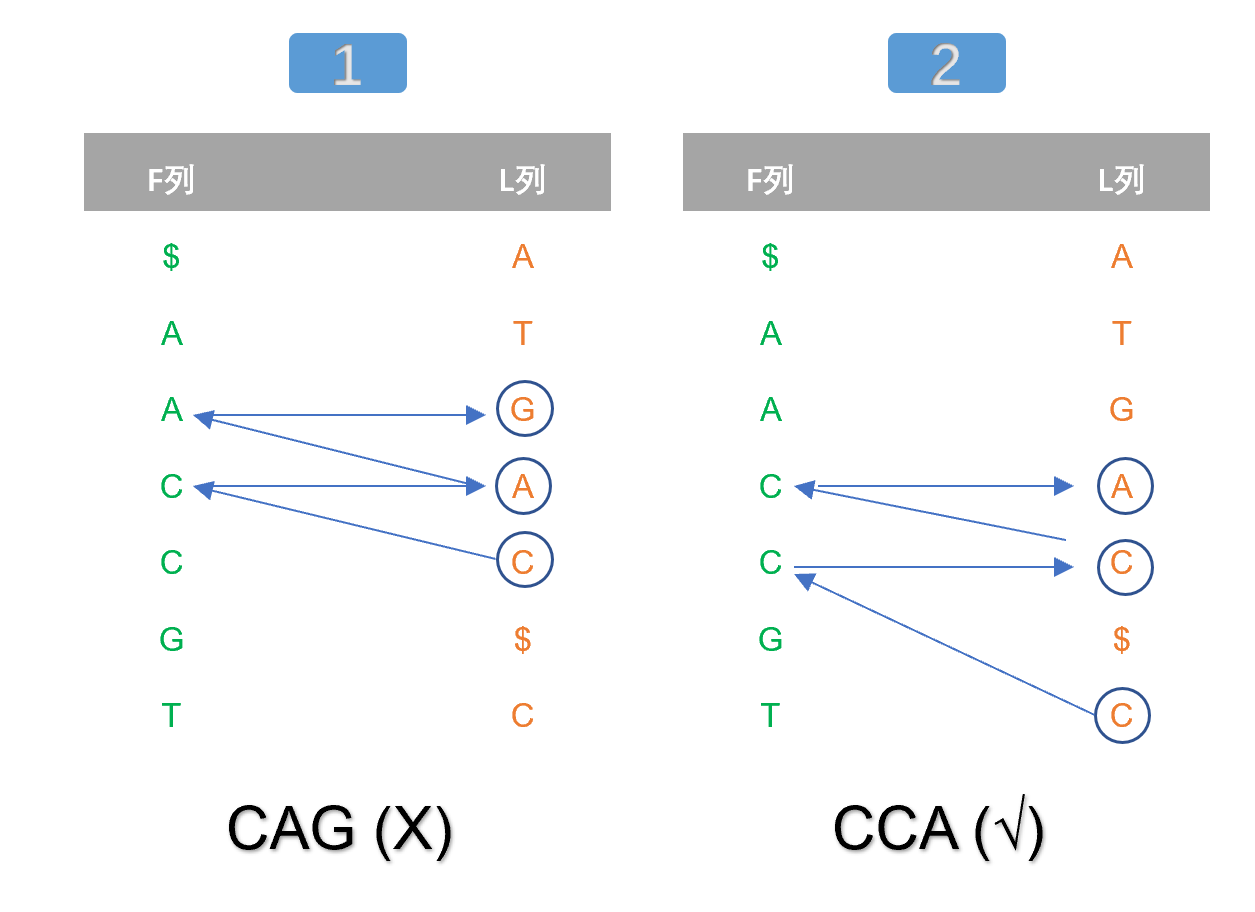
图3 序列比对推导过程
原文作者: Billy & Barney
原文链接: https://liangbilin.github.io/2020/04/25/Billy-- BWT比对算法/
版权声明: 转载请注明出处(必须保留作者署名及链接)